Scientific Programming II

Programming in Java

Unit 7 - Assignment

Problem 1

A minimum spanning tree is defined as:

Given a connected, undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees. We can also assign a weight to each edge, which is a number representing how unfavorable it is, and use this to assign a weight to a spanning tree by computing the sum of the weights of the edges in that spanning tree. A minimum spanning tree (MST) or minimum weight spanning tree is then a spanning tree with weight less than or equal to the weight of every other spanning tree. - Wikipedia

Write a method public void printMinimumSpanningTree() that prints a minimum spanning tree of a given graph, and the total cost (total of traveled weights) of the tree. A graph can have multiple minimum spanning trees that are equal in cost.

Note: These "trees" are not the binary search trees we worked with earlier. These are sub-graphs.

Sample Graph

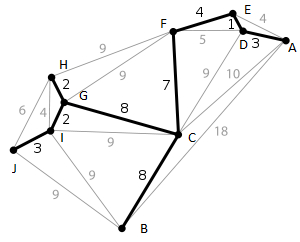
Graph graph=new Graph();
Node a=new Node(0);
Node b=new Node(1);
Node c=new Node(2);
Node d=new Node(3);
Node e=new Node(4);
Node f=new Node(5);
Node g=new Node(6);
Node h=new Node(7);
Node i=new Node(8);
Node j=new Node(9);
graph.addEdge(a,b,18);
graph.addEdge(a,c,10);
graph.addEdge(a,d,3);
graph.addEdge(a,e,4);
graph.addEdge(b,j,9);
graph.addEdge(b,i,9);
graph.addEdge(c,b,8);
graph.addEdge(c,i,9);
graph.addEdge(c,g,8);
graph.addEdge(d,e,1);
graph.addEdge(d,c,9);
graph.addEdge(d,f,5);
graph.addEdge(e,f,4);
graph.addEdge(f,c,7);
graph.addEdge(f,g,9);
graph.addEdge(f,h,9);
graph.addEdge(g,h,2);
graph.addEdge(g,i,2);
graph.addEdge(h,i,4);
graph.addEdge(h,j,6);
graph.addEdge(i,j,3);

Pseudocode for Prim's Algorithm

// Define a "Prim Edge" as an edge with one node in the spanning
// tree, and one node not

func primsAlg()
    tmp: Graph <- Graph()

    tmp.add(random node from this)

    while (tmp.nodes != this.nodes)
        tmpEdge <- smallestPrimEdge(tmp)
        tmp.edges.add(tmpEdge.A, tmpEdge.B, tmpEdge.Weight)
    endwhile

    STDOUT.println(tmp)
endfunc

func smallestPrimEdge(g: Graph)
    min: int <- 99999999;
    tmp: Edge <- random edge
    other: Set <- g.nodes

    for (edge e in edges)
        a: Node <- e.A
        b: Node <- e.B

        if (other has a and not b or
            other has b and not a)
            if (e.Weight < min)
                tmp <- e
                min <- e.Weight
            endif
        endif
    endfor

    return tmp
endfunc

Problem 2

A cycle in a graph is a series of nodes in a graph such that there is a connected path going from and leading back to the same node. Within graph theory there are several types of cycles, but we will focus solely on cycles that start and end at the same node.

Write a method public boolean hasCycles() that tests if a graph has cycles.