Scientific Programming II

Programming in Java

Binary Search Trees

Complexity

• Search

  • Average: O(log n)
  • Worst: O(n)

• Insert

  • Average: O(log n)
  • Worst: O(n)

• Delete

  • Average: O(log n)
  • Worst: O(n)

Where n is the number of stored items

So far, we have covered linked lists/deques, queues, and stacks. The common property of each of these structures is that each of them are one-dimensional. Now, we are going to begin to explore two-dimensional data structures, beginning with binary search trees.

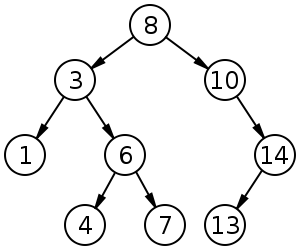
A binary search tree (BST) is a data structure where each node has two references – left and right. The value in the left reference is less than the value in the node and the value in the right reference is more than the value in the node. Typically, all values in a binary search tree are distinct. The node at the top of a BST is called the root.

Trees should have the following methods at minimum:

• public void insert(T data) - Add a value to the Tree
• public boolean isEmpty() - Test if the Tree is empty
• public void outputTree() - Print the Tree

TreeTest.java

import java.util.Scanner;

public class TreeTest
{
    public static void menu()
    {
        System.out.println("1 - Insert a Value");
        System.out.println("2 - Print the Tree");
        System.out.println("3 - Quit");
    }

    public static void main(String[] args)
    {
        System.out.println("Binary Search Trees");

        Scanner scan = new Scanner(System.in);
        Scanner scan1 = new Scanner(System.in);

        Tree tree = new Tree();
        boolean flag = true;
        int status = 0, choice = 0;

        while (flag) {
            menu();
            status = 0;

            try {
                choice = Integer.parseInt(scan.nextLine());
            } catch (Exception e) {
                System.out.println("Please choose a valid option.");
                status = 1;
            }

            if (choice == 1) {
                System.out.println("Input value");
                int input = scan1.nextInt();
                tree.insert(input);
            } else if (choice == 2) {
                tree.print();
            } else if (choice == 3) {
                flag = false;
                System.out.println("End of program");
            } else if (status == 0) {
                System.out.println("Please choose a valid option.");
            }
            System.out.println("\n");
        }
    }
}