Scientific Programming II

Programming in Java

Graded Problems

Binary Search Trees

Add the following methods in Tree.java and test the same in TreeTest.java:

  1. A method which takes the the root as the input and returns the height of the BST. The height of a BST = 1 + Maximum of (height of the left sub tree, height of the right sub tree)
  2. Write a method which outputs the values of the deepest leaf/leaves in the binary search tree.
  3. Write a method which outputs the values in the binary search tree in increasing order. (If you're getting stuck, Google in-order traversal)
  4. Write a method which prints all the non-leaf node values in the binary search tree.
  5. Write a method which prints the values in the binary search tree by level. Start by printing the value of the root (level = 1) and then values at level = 2, level = 3 and so on. (If you're getting stuck, Google level-first traversal)
  6. A complete binary tree is a special case of a binary tree, in which all the levels, except perhaps the last, are full; while on the last level, any missing nodes are to the right of all the nodes that are present. Write a function to output if an input binary search tree is complete or not.
  7. The cost of a path in a tree is sum of the values of the nodes participating in that path. Write a method that returns the cost of the most expensive path from the root to a leaf node.
  8. Build a binary search tree, T. Your program has to output all the values in the longest path in T.
    Example:
    Longest Path Example
    In this example, the longest paths are darkened for Tree_1 and Tree_2. As you can see, the longest path need not include the root. You can use arrays for this problem.
  9. Write a program that outputs all structurally distinct binary search trees of N (a positive integer > 0) nodes. Two trees are considered structurally distinct if they have different number of nodes or if their left and/or right sub trees are of different shapes. The values in the nodes are of no concern. Your program will take an integer input, N (> 0). Use the Tree.print() method to display the trees. Here is a Permutation Generator Algorithm
Deleting from a BST

In this exercise, we discuss deleting items from binary search trees. The deletion algorithm is not as straightforward as the insertion algorithm. Three cases are encountered when deleting an item:

  1. the item is contained in a leaf node (i.e., it has no children)
  2. the item is contained in a node that has one child
  3. the item is contained in a node that has two children.

If the item to be deleted is contained in a leaf node, the node is deleted and the reference in the parent node is set to null.

If the item to be deleted is contained in a node with one child, the reference in the parent node is set to reference the child node and the node containing the data item is deleted. This causes the child node to take the place of the deleted node in the tree.

The last case is the most difficult. When a node with two children is deleted, another node in the tree must take its place. However, the reference in the parent node cannot simply be assigned to reference one of the children of the node to be deleted. In most cases, the resulting binary search tree would not embody the following characteristic of binary search trees (with no duplicate values)

The values in any left subtree are less than the value in the parent node, and the values in any right subtree are greater than the value in the parent node.

Which node is used as a replacement node to maintain this characteristic? It is either the node containing the largest value in the tree less than the value in the node being deleted, or the node containing the smallest value in the tree greater than the value in the node being deleted. Let us consider the node with the smaller value. In a binary search tree, the largest value less than a parent’s value is located in the left subtree of the parent node and is guaranteed to be contained in the rightmost node of the subtree. This node is located by walking down the left subtree to the right until the reference to the right child of the current node is null. We are now referencing the replacement node, which is either a leaf node or a node with one child to its left. If the replacement node is a leaf node, the steps to perform the deletion are as follows:

The deletion steps for a replacement node with a left child are similar to those for a replacement node with no children, but the algorithm also must move the child into the replacement node’s position in the tree. If the replacement node is a node with a left child, the steps to perform the deletion are as follows:

Write a method deleteNode(int), which takes as its argument the value to delete. Method deleteNode() should locate in the tree the node containing the value to delete and use the algorithms discussed here to delete the node. If the value is not found in the tree, the method should print a message that indicates whether the value is deleted.

Source: Java Textbook (Deitel & Deitel, #17.22, Pages, 842 - 843)
Heaps

A binary max heap is a binary search tree with the following constraints:

1. All levels, except possible the last, are filled; the heap is a complete BST
2. All child nodes are all less than or equal to the parent node

Here is a visual example: 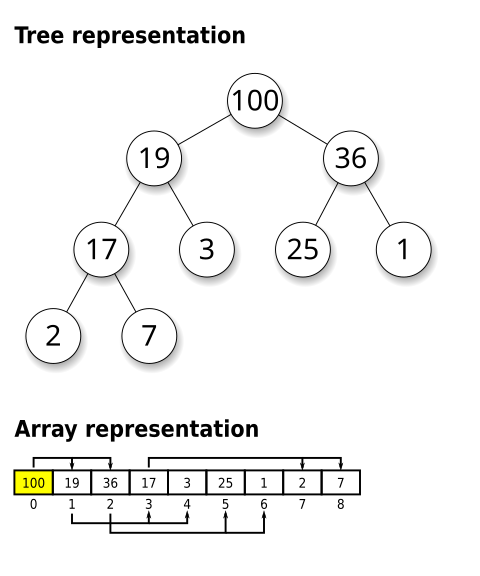Max heap example

Both the insertion and deletion operations on heaps are slightly different than a basic BST. According to Wikipedia:

Both the insert and remove operations modify the heap to conform to the shape property first, by adding or removing from the end of the heap. Then the heap property is restored by traversing up or down the heap. Both operations take O(log n) time.

The process of restoring the heap is referred to by several names, including up-heap, bubble-up, and my personal favorite percolate-up. It can be proved that this percolating process will take O(log n) time, but we will just take it on faith.

Here is the algorithm for insertion:

  1. Add the new Node to the bottom level of the Heap

  2. Compare with its parent.

Deletion, however, is slightly different. For heaps, deletions occur from the root, not from an arbitrary location in the heap. Therefore, this algorithm is as follows:

  1. Replace the root of the Heap with the last child in the last level.

  2. Compare with its children.

Graphs

Note: Graph theory can confound even the greatest programming wizards. StackOverflow and Wikipedia will guide you on your path to data structure nirvana.

Shortest Path

One of the most important problems in graph theory is how to determine the shortest path between any two nodes of a graph.

Dijkstra's Algorithm

The most famous algorithm to solve this problem is know as Dijkstra's algorithm, discovered by Edsger Dijkstra (he's Dutch!) in 1956. For a connected graph with non-negative weights, it will produce the shortest path between any two nodes.

The algorithm is as follows:

Let the node at which we are starting be called the initial node. Let the distance of node X be the distance from the initial node to X. Dijkstra's algorithm will assign some initial distance values and will try to improve them step by step.

  1. Assign to every node a tentative distance value: set it to zero for our initial node and to infinity (Integer.MAX_VALUE) for all other nodes.
  2. Set the initial node as current. Mark all other nodes unvisited. Create a set of all the unvisited nodes called the unvisited set.
  3. For the current node, consider all of its unvisited neighbors and calculate their tentative distances. Compare the newly calculated tentative distance to the current assigned value and assign the smaller one. For example, if the current node A is marked with a distance of 6, and the edge connecting it with a neighbor B has length 2, then the distance to B (through A) will be 6 + 2 = 8. If B was previously marked with a distance greater than 8 then change it to 8. Otherwise, keep the current value.
  4. When we are done considering all of the neighbors of the current node, mark the current node as visited and remove it from the unvisited set. A visited node will never be checked again.
  5. If the destination node has been marked visited (when planning a route between two specific nodes) or if the smallest tentative distance among the nodes in the unvisited set is infinity (when planning a complete traversal; occurs when there is no connection between the initial node and remaining unvisited nodes), then stop. The algorithm has finished.
  6. Select the unvisited node that is marked with the smallest tentative distance, and set it as the new "current node" then go back to step 3.
A* Algorithm

The A* algorithm (pronounced "a-star") expands upon Dijkstra's algorithm by using a 'heuristic' function. Quite simply, a heuristic function gives the A* algorithm an idea of the way to go to the target node, while Dijkstra's algorithm doesn't go in any specific direction. More specifically, Dijkstra's algorithm is the A* algorithm for which the heuristic for any node is 0, or, we have no idea if any one node is closer to our target.

The pseudocode for A* is as follows:

function A*(start,goal)
    closedset := the empty set    // The set of nodes already evaluated.
    openset := {start}    // The set of tentative nodes to be evaluated, initially containing the start node
    came_from := the empty map    // The map of navigated nodes.
 
    g_score[start] := 0    // Cost from start along best known path.
    // Estimated total cost from start to goal through y.
    f_score[start] := g_score[start] + heuristic_cost_estimate(start, goal)
 
    while openset is not empty
        current := the node in openset having the lowest f_score[] value
        if current = goal
            return reconstruct_path(came_from, goal)
 
        remove current from openset
        add current to closedset
        for each neighbor in neighbor_nodes(current)
            if neighbor in closedset
                continue
            tentative_g_score := g_score[current] + dist_between(current,neighbor)
 
            if neighbor not in openset or tentative_g_score < g_score[neighbor] 
                came_from[neighbor] := current
                g_score[neighbor] := tentative_g_score
                f_score[neighbor] := g_score[neighbor] + heuristic_cost_estimate(neighbor, goal)
                if neighbor not in openset
                    add neighbor to openset
 
    return failure
 
function reconstruct_path(came_from,current)
    total_path := [current]
    while current in came_from:
        current := came_from[current]
        total_path.append(current)
    return total_path